Cardinal Number Acquisition of Turkish Children
1Çukurova University, Institute of Social Sciences, Department of Early Childhood Education, Turkey
2Çukurova University, Faculty of Education, Department of Early Childhood Education, Turkey
Abstract
Cardinal number acquisition plays an important role in children’s sense of number. Various investigations have revealed the influence of cultural variables on cardinal number acquisition. In this research, we investigated Turkish children’s acquisition of cardinal numbers. Quantitative research method was used. The participants were 100 preschool children from four public preschools in Adıyaman, Turkey. We used the “Give me N” task with the intent of investigating children’s acquisition of cardinal numbers. We obtained data from individual interviews with children. As a result of the research, we found that 60% of the children had cardinal number acquisition, 34% were in subgroups, and 6% were in the pre-number phase. In our sample the youngest child who had acquired cardinal numbers was 45 months old. We saw that the acquisition of the cardinal number phase was between 49 and 61 months for Turkish children and the majority of children older than 62 months had acquired cardinal numbers. Turkish children have the same cardinal number acquisition levels as their western peers however they acquire cardinal numbers a bit later. This research result showed that cultural differences could have a role in the age of cardinal number acquisition but not in phases. More cross-cultural studies are needed to better understanding.
Keywords: Cardinality, Number acquisition, Counting, Give me N, Knower levels, Number words, Early childhood education, Preschoolers
JEL Classification:I29.
1. Introduction
Counting is a critical skill in the acquisition of many mathematical concepts and skills (Baroody and Price, 1983; Aunio et al., 2005). Some young children can count beginning from two years old even before they have any formal education (Bryant, 1996). However, we know that young children often make some mistakes (like skipping number words, using nonconventional lists) when they are counting (Gelman and Meck, 1983; Gelman et al., 1986; Sarnecka and Carey, 2008; Sarnecka and Lee, 2009) . The process by which children become competent in counting is explained with two different theories by researchers. Piaget (1984) stated that counting is not a mathematical process for young children before they have number conservation. Researchers who followed him such as Fuson, Richards, and Briars called this process “context specific meaning” (Fuson et al., 1982). On the other hand, Gelman and Gallistel argued that preschoolers do have a concept of number – a concept that contains many of the seeds from which modern arithmetic has grown – and that even very young children can count small groups (two to four objects) (Gelman and Gallistel, 1978). They stated that the mistakes of young children when they are counting are caused by the method these authors used and by cardinal numbers. In addition to these results, subsequent researchers have revealed the influence of culture in cardinal number acquisition (Campbell and Xue, 2001; Sarnecka et al., 2007; Aunio et al., 2014; Cankaya et al., 2014) . In this study, we aimed to contribute to the discussion in the literature by examining the acquisition of cardinal numbers by Turkish children.
1.1. Theoretical Framework
In the preschool period, children encounter many basic concepts related to mathematics (Aktaş-Arnas et al., 2003) and one of these basic mathematical concepts is numbers. Children can use number words from very early years. However, using the number words in correct order does not prove that young children have number concept (Olkun et al., 2013). Number acquisition has an important role for children’s further education both formal and informal. Therefore, it plays a critical role in the early years (Olkun et al., 2013).
Cardinal numbers are used to determine the quantitative value of a group. The acquisition of cardinal numbers requires some skills such as memorizing number words and, some kinds of mathematical skills such as classification, sorting, and matching number words with quantities (Ginsburg and Ertle, 2008). To count a mascot, cup and book on a table, all the number words must first be known, and then, all the objects on the table must be counted. During the counting process, the cup may match with “one”, the book “two” and the mascot “three”. In a different counting, the mascot may match with “one, the cup “two” and the book “three”. No one matches the word “cup” to “mascot” or “book” in colloquial conversation. In contrast to other words, number words belong to a group because the final count word indicates the number of objects in the set as a whole-total quantity. For instance, when we count this group, we use “one” for cup, “two” for book and “three” for mascot; the number word “three” does not belong to “mascot”, it belongs to the group itself. According to Ginsburg and Ertle (2008) this perception underlies cardinal number acquisition.
Piaget in his conservation task showed children to two arrays of tokens (both of them having the same number) and asked them “Which array has more tokens?” (Piaget, 1984). Young children often said that the array that occupied more space contained more tokens than the other array even if they counted both. Although there are two different logical ways to solve this problem from Piaget's point of view, young children mostly choose the third and non-logical way. The first way is to count the two arrays; the second one, to match them together; and the third, the non-logical one, to think that the longer one contains a greater number (Piaget, 1984). Piaget interpreted this situation as an intuitive thought directing the child’s thinking. According to Piaget, children cannot count logically before they gain number conservation (approximately six years old) (Önkol, 2010).
In contrast to Piaget's claims, Gelman and Gallistel (1978) argued that even very young children can count. Gelman and Gallistel stated that “When we say that a young child counts, we do not necessarily mean that the child follows the adult pattern.” They thought children do not have to use conventional number words nor conventional order. When they recorded young children counting sequences, they saw various counting sequences. Because of these nonconventional number word sequences, Gelman and Gallistel (1978) believed that a young child’s ability to count is governed by the implicit knowledge of several principles. These are the (1) “one-to-one principle”; (2) “stable order principle”; (3) “cardinal principle”; (4) “abstraction principle”; and (5) “order irrelevance principle”. According to Gelman and Gallistel (1978) these principles lead children’s counting. They stated that before children learn counting, they already know these principles and that these implicit principles lead to children counting (Gelman and Meck, 1983). They provide two lines of evidence to prove their claims.
First, research showed that even babies can distinguish numerosity (Gelman, 1977; Starkey et al., 1983; Xu and Spelke, 2000) . For instance, Antell and Keating (1983) found that neonates (average 53 hours, 40 neonates) can understand the difference in number between two cards. Second, it appears that mistakes made by young children are mostly idiosyncratic. For example, according to Gelman and Meck (1983) a child can count a three-element row as "1-2-8" a four-element row as "1-2-8-10". Another mistake is sorting number words as "1-2-3-4-5-6-7-h-i-j-k" or "1-2-3-4-5-6-7-8-red-yellow-blue”. In this case, although the number words in the memories of the young children are limited, they seem to produce their own nonconventional counting list and they use first three counting principles. Therefore, Gelman and Gallistel (1978) indicated that children are using different counting patterns than adults but this usage does not mean that children cannot count. They conclude that this pattern is the result of implicit information directing a child’s counting and that the child searches for a list instead of complete the counting.
Gelman and Gallistel asked children to use counting in a single row but Piaget asked to compare the number of members in two different rows (Bryant, 1996). The main difference between the two methods is that Gelman and Gallistel (1978) focus on the counting one set a time, while Piaget (1984) focuses on the relation between sets. Therefore, the Piaget method is more challenging than the Gelman method (Bryant, 1996). Researchers (Saxe, 1977; Michie, 1984; Sophian, 1988) stated that even some children who can count easily do not know how to use numbers to compare two different groups. In Sophian (1988) study, for instance, children three and four years old watched a puppet count objects in two rows. In the first trial, the experimenter wanted the puppet to answer which row had more objects. In the second trial, the experimenter wanted the puppet to answer how many objects there were. The puppet made some mistakes deliberately. For instance, when the experimenter asked which row had more, the puppet counted both groups. When the experimenter asked how many objects there were, the puppet counted just one row. The experimenter asked questions to the children; “Which puppet has done it right?” and “Which puppet has done it wrong?” (Sophian, 1988). Sophian found that even if children can understand the correctness of counting, they cannot understand that two groups must be counted separately to make comparisons (1988). Considering these findings, she claimed that children do not use numbers to make comparisons (Sophian, 1988). Bryant (1996) supposed that these findings contribute to Piaget’s view. Bryant (1996) argued that the reason why children cannot understand the erroneous actions of the puppets arises from the fact that even if children can understand that the last number word expresses the number of members of the group, children cannot understand cardinal meanings.
To explain this situation, Fuson et al. (1982) proposed “context specific meaning” based on Piaget’s views. Fuson et al. (1982) stated that “young children hear number words that vary in meaning according to the contexts in which they are used, and early in their learning of these words, children build up separate, context-specific areas of meaning and as children age, these areas begin to connect”. These authors claimed that number words have different meanings for young children. When children have more experience with counting, they begin to connect these meanings. Researchers who advocate this view think that children cannot know the cardinal meaning of number words even if they can correctly count two rows in Piaget’s experiment (Fuson et al., 1982; Fuson, 1988). Fuson described this situation as “last-word responding” (1988). According to Fuson, when we ask children how many objects are there, even if they replied correctly, the final number word given as the answer to the question may not refer to cardinality for young children. Counting the sounds of drum taps, three-dimensional objects, objects lined up in a straight line, or objects arranged in a circle requires different procedures and skills. When children have these experiences, they become masters of counting by compounding all the routines. As a result, the researchers claimed that children first learned to count and then learned counting principles (Fuson et al., 1982; Siegler and Robinson, 1982; Fuson, 1988).
Besides all these, Wynn (1990) suggested that the “ultimate test of the two theories must concentrate on whether very young children do in fact understand cardinality”. The one-to-one correspondence and stable-order principles among counting principles are skills that even very young children can accomplish in the direction of their cognitive capacities; however, the cardinality principle is different from the one-to-one correspondence and stable-order principles (Wynn, 1990). It is directly related to counting and mathematical ability (Wynn, 1990). Thus, Wynn (1990) developed a task named “Give me N” (e.g., “Could you give the puppet five dinosaurs?”) to test children’s understanding of cardinal numbers. In this task, the experimenter asks children to put a specific number of toys on a tray for the puppet. Wynn has found that children who can show five or more correct numbers of toys can show all the numbers they used. Therefore, children who are able to show only “five” or more correctly in Wynn’s method are considered to have cardinal acquisition. Wynn stated that even if children use number words earlier, they perform cardinal number acquisition at approximately 3.5 years of age and that they do not comply with the cardinal number principle before. According to Wynn (1990) these findings support the work of Fuson (1988).
Various researchers have supported context-specific meaning and suggest that children initially do not understand the cardinal number principle. In addition, they argue that implicit principles that lead to children counting cannot be proved (Baroody and Price, 1983; Fuson, 1988; Wynn, 1990; Bryant, 1996; Le Corre and Carey, 2007; Sarnecka and Carey, 2008; Nikoloska, 2009) . However, there are some unanswered questions even for researchers supporting this view (Wynn, 1992). For example, “How can children succeed in small groups?” or “How do children come to understand that counting is related to numerosity?” (Wynn, 1992).
Subsequent researchers have raised the notion of the “Knower Level” in response to all these problems (Condry and Spelke, 2008; Sarnecka and Lee, 2009). According to this idea, “children learn the number-word meaning in an order” (Sarnecka and Lee, 2009). These levels are “pre-number”, “1 knower”, “2 knower”, “3 knower”, “4 knower” and “Cardinal principle knower”. To exemplify these levels, if a child is at the 4 knower level, s/he knows the meaning of 4 and smaller numbers but does not know 5 and higher numbers even if s/he can verbally use these numbers. At this point, the cardinality associated with the number words is still represented by a system based on memorization (Le Corre et al., 2006; Le Corre and Carey, 2007; Sarnecka and Lee, 2009) .
1.2. Problem
Consequently, current researchers have revealed that even if children can perform counting, up to a certain age, they do not know the cardinal meaning of numbers. However, even for children who do not know cardinality, it appears that the numbers are not completely distinct from a quantitative sense (Wynn, 1990; Gallistel and Gelman, 1992; Le Corre and Carey, 2007; Sarnecka and Lee, 2009) . In addition to this, studies in the literature are seen to be carried out mostly in western cultures and with English-speaking children. Studies in different languages and cultures may provide new perspectives on the current debate.
Several studies have showed importance of language in math (Miller and Stigler, 1987; Miller et al., 1995; Lefevre et al., 2002; Barner and Bachrach, 2010; Krinzinger et al., 2011; Wagner et al., 2015) . Specifically for number acquisition, Wynn (1992) found that all children were successful at "1". However, it is unclear whether this is because children know singularity and plurality in English or because they know the meaning of the number "1". To understand this Sarnecka and her friends tested children who speak Japanese, English and Russian by Give me N task and indicated that learning of "one", "two", "three" is supported by the conceptual framework of grammatical rather than integers (Sarnecka et al., 2007; Sarnecka, 2014). Le Corre et al. (2016) stated that prior knowledge of the numerical meaning of the distinction between singular and plural supports the acquisition of the meaning of “one”. In Turkish, there is no clue about singularity or plurality when pointing to a certain number of objects, the sentence structure is always the same (i.e. give me one/two/three/four/five banana, not bananas/ only the number changes) and therefore it is important to examine cardinal number acquisition of Turkish children.
In addition, there are differences in the number naming system between the Turkish and English languages. The Turkish number naming system is more regular than the English number naming system. Similarly, the Chinese number naming system is also more regular than that of English and several studies have revealed that Chinese children performed better than western peers in arithmetic (Miller and Stigler, 1987; Ryoo et al., 2014; Li et al., 2015) . In English, after 10, the number words progress in the form of "ten, eleven, twelve", whereas in Turkish, they progress in the form of "ten, ten-one, ten-two" (in Turkish, “on, on-bir, on-iki”). Differences in language structure can play an important role in children's acquisition of numbers (Miller et al., 1995; Lefevre et al., 2002; Göbel et al., 2011; Krinzinger et al., 2011; Cankaya et al., 2014) .
Every child develops his or her mathematical skills and knowledge in a particular cultural context and this context defines what constitutes mathematical thinking and practice (Benigno and Ellis, 2008). Cultural context such as traditional games, fairy tales, story books, cradle-songs and children daily routine may have important role on the number acquisition (Civil, 2002; Street et al., 2005). For example Anderson et al. (2004) indicated that shared reading activities affect children’s math abilities. Further, Vygotsky (1998) emphasized the importance of language and culture in cognitive development. All these reasons led us to investigate the cardinal number acquisition of Turkish children. In this research, we tried to find answers to the following questions by focusing on the acquisition of cardinal numbers in Turkish children.
- At which age is cardinal number acquisition typically detected in Turkish children?
- What is the level of acquisition of cardinal numbers in Turkish children between 35 and 76 months?
2. Method
This study was conducted to examine cardinal number acquisition of Turkish children. Therefore quantitative research method was used. To clarify children number acquisition, descriptive research method was utilized.
2.1. Participants
The study participants were 100 children (46 boys, 54 girls), aged on average 56 months (SD = 10.76 months, age range 35-76 months). The participants were obtained from four preschools in Adıyaman in Turkey. Preschools are selected with purposive sampling because of the difficulties by reaching young children. Adıyaman, located in Turkey’s South-eastern Anatolia, is a city of 245 thousand inhabitants. Although there are children in Adıyaman who can speak both Turkish and Kurdish, the participants were selected only from Turkish-speaking children. The data were collected in April-May 2017. The children were divided into 6 groups according to ages to examine changes between cardinal number acquisition and age. There were 35-41 months (n=10), 42-48 months (n=16), 49-54 months (n=17), 55-61 months (n=18), 62-68 months (n=23) and 69-76 months (n=16). The children’s parents were at the middle class socioeconomic level.
An academic year in Turkey consists of two semesters. The academic year begins in September and ends in June. The children were taught in the framework of the curriculum determined by the Turkish Ministry of National Education (MEB). The curriculum is developmental and intended to support the preschool children in six developmental areas (social and emotional, motor, cognitive, literature, language and self-care) (Anonymous, 2013). This curriculum includes learning outcomes such as “S/he can count the objects” and “S/he can show the specified number of objects”. Thus, according to the Turkish Ministry of National Education, the task used in this study was suitable for preschool.
2.2. Measure
Give Me N Task. The cardinal number acquisition of children was measured in the "Give me N" task developed by Wynn (1990). Wynn had used this task with “Big Bird” (from Sesame Street), plastic toys and a tray. Since the Sesame Street TV program is not aired on Turkish television today, we used the plush toy of the character “Yoohoo” (Yoohoo and Friends) which is broadcast on TRT Çocuk (Turkey Radio and Television Chanel - Kids) and widely watched by children. We used small stones instead of plastic toys and the stones were colour and shine, they were like come from utopia in cartoon. During the interview, the investigator had simple and relaxing conversations with the children about them and then asked the children “This is my friend Yoohoo, and these are his stones. He needs your help. Can you help him? He wonders how many stones he has. Can you put two stones in the tray?” If child could achieve the exact number asked by the researcher, the researcher asks the child for a higher value. Otherwise, the researcher asks for a lower value. The children who can put together five or six stones correctly into the tray are accepted as cardinal number knower children. The researchers suggested that, children who acquired cardinal numbers understand how counting works (Le Corre et al., 2006; Nikoloska, 2009; Sarnecka and Lee, 2009) . Wynn (1990) indicated that these children can put together all of the numbers they know.
2.3. Procedure
One of the researchers was involved an indoor activity with the children before an interview; then, the researcher and child went to a quiet place. The researcher asked the child: “Hi, this is my friend Yoohoo; do you want to meet him?”, “Can you tell your name to Yoohoo?”, and “Do you like him?” When the child began to speak, the researcher asked “My friend Yoohoo has a problem. Would you like to help him?”, “Can you count these stones for him?”, “He wonders how many stones he has?”, and “He needs three stones. Can you take three stones and put them in the tray?” The answers given by the children were recorded by the researcher with an entry form.
2.4. Data Analysis
To describe cardinal number acquisition, frequency percentages and mean values were used. Additionally, graphical analysis was used to evaluate the skill acquisition of the groups. Graphical analysis is a frequently used method of data analysis in the acquisition of skills, especially in special education (Kırcaali-Iftar and Tekin, 1997). With the help of graphical analysis in special education, the percentage of a child's ability to perform the target skill correctly during the course is calculated, and the result is obtained when the student exceeds the percentage determined by the researcher. In this study, the percentage of acquiring a skill in a certain age group instead of a single child was calculated and shown by a line graph.
3. Results
This research was conducted to investigate the acquisition of cardinal numbers in Turkish children. The findings are presented in tables and graphs. Table 1 shows the percentages of children acquiring cardinal numbers.
Table-1. Acquisition of children’s cardinal numbers
Knower Level |
||||||
No Response |
1 Knower |
2 Knower |
3 Knower |
4 Knower |
Cardinal Number Knower |
|
Frequency |
6 |
2 |
8 |
12 |
12 |
60 |
Percentage (%) |
6 |
2 |
8 |
12 |
12 |
60 |
Source: Data have obtained from authors’ field study.
Sixty percent of the children had cardinal number acquisition, 34% of the children were in subgroups, and 6% of the children were at the pre-number level. Among the children in the subgroups, two children put together one object, eight children put together two objects, 12 children put together three objects, and 12 children put together four objects. Four pre-number-level children used number words but did so incorrectly. Two of them did not use any number words or counting process.
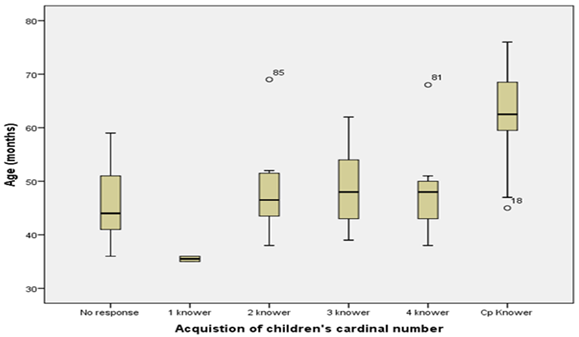
Figure-1. Shows a box plot chart for the acquisition of children’s cardinal numbers.
Source: Figure has obtained from authors’ field study.
In Figure 1, the rectangular boxes represent 50% of the children in the group. The underlines indicated 25% of the children in the group above, and the top line showed 25% of the children in the group below. The lines in the box represent the median of the group, and the circles showed extremes. The pre-number level children were between 36 and 49 months (X= 44 months), the children at the “1 knower” level were between 36 and 45 months (X =35.5 months), the children at the “2 knower” level were between 38 and 69 months (X =46.5 months), the children at the “3 knower” level were between 39 and 62 months (X =48 months) and the children at the “4 knower” level were between 38 and 68 months (X =48 months). The children who had achieved cardinal number acquisition ranged between 45 and 76 months old (X =62.5 months). The youngest children in the five different subgroups (pre-number, 1 knower, 2 knower, 3 knower and 4 knower) ranged in age from 36 to 39 months, while the youngest child who achieved cardinal number acquisition was 45 months old.
To determine the cardinal number acquisition of children according to age groups, cross-tabulation was performed, and the cardinal number acquisition levels of the groups are presented in Table 2.
Table-2. Levels of cardinal number acquisition according to age groups
Cardinal number acquisition |
||||||||
No Response |
1 knower |
2 knower |
3 knower |
4 knower |
Cardinal Principle knower |
Cardinal Principle |
Total |
|
Knower % |
||||||||
35-41 |
2 |
2 |
1 |
2 |
3 |
0 |
0 |
10 |
42-48 |
2 |
0 |
4 |
4 |
4 |
2 |
12 |
16 |
49-54 |
1 |
0 |
2 |
3 |
4 |
7 |
41 |
17 |
55-61 |
1 |
0 |
0 |
2 |
0 |
15 |
83 |
18 |
62-68 |
0 |
0 |
0 |
1 |
1 |
21 |
91 |
23 |
69-76 |
0 |
0 |
1 |
0 |
0 |
15 |
93 |
16 |
Total |
6 |
2 |
8 |
12 |
12 |
60 |
60 |
100 |
Source: Data have obtained from authors’ field study.
As shown in Table 2, none of the children between 35 and 41 months achieved cardinal number acquisition. Twelve percent of the children in the 42-48 months group, 41% of the children in the 49-54 months group, 83% of the children in the 55-61 months group, 91% of the children in the 62-68 months group and 93% of the children in the 69-76 months group achieved cardinal number acquisition.
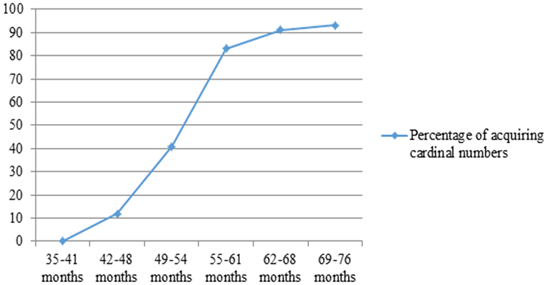
Figure-2. Percentage of acquiring cardinal numbers for the age groups
Source: Figure has obtained from authors’ field study.Figure 2 shows the percentage of children who acquired cardinal numbers in each age group. The vertical axis represents the percentage of cardinal number acquisition while the horizontal axis shows age groups. The rate of cardinal number acquisition increased with age. None of children achieved cardinal number acquisition before 45 months old. The children from 49-54 months old had approximately four times better performance than children from 42-48 months old in the cardinal number acquisition rate. The children from 55-61 months old had approximately two times better performance than in children from 49-54 months old. This finding led us to conclude that there is a common period of cardinal number acquisition in Turkish children, which is between ages of 42 and 61 months.
The majority of children were first attaining cardinal number acquisition in the 55-61 month age range. This finding can be interpreted as the fact that the children in the study group typically achieved cardinal number acquisition at 55-61 months. There was an increase in the rate of acquiring cardinal number with age, but after the 55-61 months range, the rate of increase significantly decreased. This finding confirms that children in the study group typically achieved cardinal number acquisition at 55-61 months.
4. Discussion
In this study, the cardinal number acquisition of Turkish children was investigated. Sixty percent of the children in the sample performed cardinal number acquisition, 34% were in the subgroups, and 6% were at the pre-number level. The youngest child who achieved cardinal number acquisition was 45 months old. The average age of cardinal number acquisition was 55-61 months. Additionally, children 42-48 months and 55-61 months showed a significant increase in cardinal number acquisition. Moreover, unlike the other studies in western cultures, six children were at the pre-number level and could not even put together “1” object.
When the literature is examined, it is seen that the youngest child to achieve cardinal number acquisition is between 34 and 46 months. Give me N task was used in all these studies. For example, Wynn (1990) tested 24 children between the ages of 28 and 43 months and stated that the acquisition of cardinal numbers began to appear at approximately 42 months. Sarnecka and Carey (2008) tested 73 children aged from 34 months to 51 months. They stated that the youngest child who acquired cardinal number was 35 months old and the average age of children who acquired cardinal numbers was 44 months. Le Corre et al. (2006) tested 50 children aged between 25 and 49 months and found that the mean age of children with cardinal number acquisition was 44 months and the youngest child who acquired cardinal numbers was 34 months old. Batchelor et al. (2015) tested 60 children aged between 31 months and 58 months and found that 23 children achieved cardinal number acquisition. Besides all these, Condry and Spelke (2008) found that none of the 32 children aged between 37 and 42 months in their studies achieved cardinal numbers. Nikoloska (2009) stated that 37 of 68 Macedonian children were achieved cardinal number acquisition. The youngest child who acquired cardinal number was 46 months old, and the average age was 54 months old.
The difference in the youngest age of cardinal number acquisition can be caused by the language, the number naming system, and cultural differences. For example, Sarnecka et al. (2007) conducted a study with 70 children from the United States (English-speaking), 44 children from Russia, and 48 children from Japan to measure the impact of different languages and cultures. The researchers found that Japanese-speaking children acquired cardinal numbers later than their English- and Russian-speaking peers. Lefevre et al. (2002) applied four number tasks to English speaking Canadian and French children and the results showed that children who speak French performed more poorly on the rote-counting and number-recognition tasks than English speaking preschoolers. Researchers indicated importance of language (number naming system) and culture. Cankaya et al. (2014) investigated the influence of number-naming on early numeracy in English-speaking children and in Turkish-speaking children. They concluded that a regular number naming system was effective in learning numbers.
In this study, 34% of the children answered correctly when one, two, three and four stones requested, but when five and six stones were requested, they made mistakes. The development of children’s cardinal number acquisition in this situation is a different debate. Wynn (1990) first used the phrase “grabbers” for these children while subsequent researchers used “knower levels” (Nikoloska, 2009; Sarnecka and Lee, 2009). Sarnecka and Lee (2009) examined the answers of the children who knew “1”, “2”, “3” and “4” but did not know “5” or “6”. They found that most of these children could count to 10 but they did not know the cardinal value of numbers. They stated that children’s mistakes in the study were not due to performance, but that there was a conscious guessing mistake. For example, when they asked a child to give them six objects, children never gave one, two, three or four objects even if they did not know exactly the cardinal value of six objects.
In the current study, we reached same results as Sarnecka and Lee (2009). When we examined answers from the subgroups, we observed that these children’s mistakes were conscious guessing mistakes. Therefore, we think that Turkish children have a trajectory of cardinal number acquisition similar to that of their western peers (Carey, 2001; Carey, 2004; Condry and Spelke, 2008; Sarnecka and Lee, 2009) . In this study, the youngest children in the pre-number level and subgroups ranged between 36 and 39 months of age, and the youngest child who achieved cardinal number acquisition was 45 months old. There was a gap of seven months between the youngest child who achieved cardinal number acquisition and the youngest child who was in the 4 knower level. This finding supports the fact that children who know between 1 and 4 do not have cardinal number acquisition and children who know 5 or more have cardinal number acquisition.
Wynn (1992) found that all children were successful when they were asked to give “1” object. However, she was not sure whether children knew the meaning of the number “1” or they merely knew how to use the singular and plural structure of the English language. Sarnecka et al. (2007) claimed that young children learning of "one", "two", "three" are supported by the conceptual framework of grammatically rather than integers. Le Corre et al. (2016) have investigated to English speaking and Mandarin speaking young children’s number acquisition to determine whether singular/plural morphology supports to acquisition of number word "one". Researchers concluded that the numerical meaning of distinction between singular and plural morphology supports the acquisiton of the meaning of the number word for one (Le Corre et al., 2016). We did not have enough evidence to say it is the same for Turkish children yet six children in this study could not respond to any request correctly and they failed even when “1” object was requested. Four of them used number words to count but still failed to show “1” object. We considered that children are not aware of the quantitative value of the number of “one” rather than the lack of concepts related to quantity, since there is no singularity or plurality to mark specific number of objects (i.e. Give me one/two/three/four/five object-that's all same in Turkish).
5. Conclusion
This study was conducted to investigate Turkish children’s cardinal number acquisition. We used Give N task to measure it cardinal number acquisition of children. We found that 60% of the children in the sample achieved cardinal number acquisition and the youngest child with cardinal numbers in the study group was 45 months of age. There was a significant increase in cardinal number acquisitions in children from 49 to 61 months old. We state that this age range is a phase in which Turkish children acquire cardinal numbers. Most of the children who were older than 62 months old had achieved cardinal number acquisition. Unlike the past studies conducted in western cultures, in the current study, there were some children who could use number words but did not know even the cardinal value of the number “1”. We concluded that even if children use number words, they are unaware of cardinal value of number words at the beginning. However, the mistakes of children in the subgroups were conscious guessing mistakes because when higher values were asked, they did not give lower number. Therefore, we think that Turkish children have the same cardinal number acquisition levels as their western peers such as 1 knower, 2 knower, 3 knower, 4 knower, and cardinal knower.
Further research may investigate cardinal number acquisition in different cultures and languages. Studies involving parents and home environments can offer researchers new insights, so educators can find the best way to support early cardinal number development in children. Intervention programs may be developed to support the acquisition of cardinal numbers at an early age. Having cardinal number acquisition in the early years will offer the child many mathematical opportunities.
References
Aktaş-Arnas, Y., E. Deretarla-Gül and A. Sığırtmaç, 2003. Validity and reliability study of the number and operation concepts and skills test for 48–86 months old children. Cukurova University Institute of Social Sciences, 12(12): 147-157.
Anderson, A., J. Anderson and J. Shapiro, 2004. Mathematical discourse in shared storybook reading. Journal for Research in Mathematics Education, 35(1): 5-33. Available at: https://doi.org/10.2307/30034801.
Anonymous, 2013. Turkis national preschool program. Ankara: Publications of Turkish Ministry of National Education.
Antell, S. and D. Keating, 1983. Perception of numerical invariance in neonates. Child Development, 54(3): 695-701. Available at: https://doi.org/10.2307/1130057.
Aunio, P., J. Hautamäki and J.E. Van Luit, 2005. Mathematical thinking intervention programmes for preschool children with normal and low number sense. European Journal of Special Needs Education, 20(2): 131-146. Available at: https://doi.org/10.1080/08856250500055578.
Aunio, P., J. Korhonen, L. Bashash and F. Khoshbakht, 2014. Children's early numeracy in Finland and Iran. International Journal of Early Years Education, 22(4): 423-440. Available at: https://doi.org/10.1080/09669760.2014.988208.
Barner, D. and A. Bachrach, 2010. Inference and exact numerical representation in early language development. Cognitive Psychology, 60(1): 40-62. Available at: https://doi.org/10.1016/j.cogpsych.2009.06.002.
Baroody, A.J. and J. Price, 1983. The development of the number-word sequence in the counting of three-year-olds. Journal for Research in Mathematics Education, 14(5): 361-368. Available at: https://doi.org/10.2307/748681.
Batchelor, S., S. Keeble and C. Gilmore, 2015. Magnitude representations and counting skills in preschool children. Mathematical Thinking and Learning, 17(2-3): 116-135. Available at: https://doi.org/10.1080/10986065.2015.1016811.
Benigno, J. and S. Ellis, 2008. Do parents count? The socialization of children's numeracy. In O. Saracho, & B. Spodek, Contemporary Perspectives on Mathematics in Early Childhood Education. Charlotte NC: Information Age Publishing. pp: 291-308.
Bryant, P., 1996. Children and arithmetic. In L. Smith, Critical Readings on Piaget. New York: Taylor & Francis e- Library. pp: 312-346.
Campbell, J. and Q. Xue, 2001. Cognitive airthmetic across cultures. Journal of Experimental Psychology, 130(2): 299-315. Available at: https://doi.org/10.1037//0096-3445.130.2.299.
Cankaya, O., J.-A. LeFevre and K. Dunbar, 2014. The role of number naming systems and numeracy experiences in children's rote counting: Evidence from Turkish and Canadian children. Learning and Individual Differences, 32: 238-245. Available at: https://doi.org/10.1016/j.lindif.2014.03.016.
Carey, S., 2001. Cognitive foundations of arithmetic: Evolution and ontogenesis. Mind & Language, 16(1): 37-55. Available at: https://doi.org/10.1111/1468-0017.00155.
Carey, S., 2004. Bootstrapping and the origins of concepts. Daedalus, 133(1): 59-68. Available at: https://doi.org/10.1162/001152604772746701.
Civil, M., 2002. Culture and mathematics: A community approach. Journal of Intercultural Studies, 23(2): 133-148. Available at: https://doi.org/10.1080/07256860220151050a.
Condry, K. and E. Spelke, 2008. The development of language and abstract concepts: The case of natural number. Journal of Experimental Psychology: General, 137(1): 22-38. Available at: https://doi.org/10.1037/0096-3445.137.1.22.
Fuson, K., 1988. Children's counting and concepts of number. New York: Springer Verlag.
Fuson, K., J. Richards and D. Briars, 1982. The acquisition and elaboration of the number word sequence. In C. Brainerd, Springer series in cognitive development; children's logical and mathematical cognition. New York: Springer-Verlag. pp: 33-92.
Gallistel, C.R. and R. Gelman, 1992. Preverbal and verbal counting and computation. Cognition, 44(1-2): 43-74. Available at: https://doi.org/10.1016/0010-0277(92)90050-r.
Gelman, R., 1977. How young children can reason abaout small numbers. In N. Castellan, D. Pisoni, & G. Potts, Cognitive Theory. New Jersey: Hillsdare.
Gelman, R. and C. Gallistel, 1978. The child's understanding of number. Harvard: Harvard University Press.
Gelman, R. and E. Meck, 1983. Preschoolers' counting: Principles before skill. Cognition, 13(3): 343-359. Available at: https://doi.org/10.1016/0010-0277(83)90014-8.
Gelman, R., E. Meck and S. Merkin, 1986. Young children's numerical competence. Cognitive Development, 1(1): 1-29. Available at: https://doi.org/10.1016/s0885-2014(86)80021-1.
Ginsburg, H. and B. Ertle, 2008. Knowing mathematics in early childhood mathematics. In O. Saracho, & B. Spodek, Contemporary Perspectives on Mathematics in Early Childhood Education. Charlotte NC: Information Age Publishing Inc. pp: 45-66.
Göbel, S.M., S. Shaki and M.H. Fischer, 2011. The cultural number line: A review of cultural and linguistic influences on the development on number processing. Journal of Cross-Cultural Psychology, 42(4): 543-565. Available at: https://doi.org/10.1177/0022022111406251.
Kırcaali-Iftar, G. and E. Tekin, 1997. Single subject research methods. Ankara: Turkish Psychological Association Publications.
Krinzinger, H., J. Gregoire, A. Desoete, L. Kaufmann, H. Christoph-Nuerk and K. Willmes, 2011. Differantial language effects on numerical skills in second grade. Jornal of Cross-Cultural Psychology, 42(4): 614-629. Available at: https://doi.org/10.1177/0022022111406252.
Le Corre, M. and S. Carey, 2007. One, two, three, four, nothing more: An investigation of the conceptual sources of the verbal counting principles. Cognition, 105(2): 395-438. Available at: https://doi.org/10.1016/j.cognition.2006.10.005.
Le Corre, M., P. Li, B.H. Huang, G. Jia and S. Carey, 2016. Numerical morphology supports early number word learning: Evidence from a comparison of young Mandarin and English learners. Cognitive Psychology, 88: 162-186. Available at: https://doi.org/10.1016/j.cogpsych.2016.06.003.
Le Corre, M., G. Van De Walle, E.M. Brannon and S. Carey, 2006. Re-visiting the competence/performance debate in the acquisition of the counting principles. Cognitive Psychology, 52(2): 130-169. Available at: https://doi.org/10.1016/j.cogpsych.2005.07.002.
Lefevre, J.-A., T. Clarke and A.P. Stringer, 2002. Influences of language and parental involvement on the development of counting skills: Comparisons of French-and English-speaking Canadian children. Early Child Development and Care, 172(3): 283-300. Available at: https://doi.org/10.1080/03004430212127.
Li, X., L. Chi, M. DeBey and A. Baroody, 2015. A study of early childhood mathematics teaching in the United States and China. Early Education and Development, 26(3): 450-478. Available at: https://doi.org/10.1080/10409289.2015.994464.
Michie, S., 1984. Why preschoolers are reluctant to count spontaneously. British Journal of Developmental Psychology, 2(4): 347-358. Available at: https://doi.org/10.1111/j.2044-835x.1984.tb00942.x.
Miller, K.F., C.M. Smith, J. Zhu and H. Zhang, 1995. Preschool origins of cross-national differences in mathematical competence: The role of number-naming systems. Psychological Science, 6(1): 56-60. Available at: https://doi.org/10.1111/j.1467-9280.1995.tb00305.x.
Miller, K.F. and J.W. Stigler, 1987. Counting in Chinese: Cultural variation in a basic cognitive skill. Cognitive Development, 2(3): 279-305. Available at: https://doi.org/10.1016/s0885-2014(87)90091-8.
Nikoloska, A., 2009. Development of the cardinality principle in Macedonian preschool children. Psihologija, 42(4): 459-475. Available at: https://doi.org/10.2298/psi0904459n.
Olkun, S., E. Fidan and A. Babacan-Özer, 2013. The development of number concept and the use of counting in problem solving of 5-7 year olds. Education and Science, 38(169): 236-248.
Önkol, F., 2010. Turkish adoptation of the early numeracy test and to investigate effects of the number development the early numeracy programme for the six year old children. Doctoral Thesis. İstanbul: Marmara University/ Instute of Educational Science.
Piaget, J., 1984. Genetic epistemology. (A. Cengizkan, Trans.). Ankara: Individual and Society Publications.
Ryoo, J.H., V.J. Molfese, R. Heaton, X. Zhou, E.T. Brown, A. Prokasky and E. Davis, 2014. Early mathematics skills from prekindergarten to first grade: Score changes and ability group differences in Kentucky, Nebraska, and Shanghai samples. Journal of Advanced Academics, 25(3): 162-188. Available at: https://doi.org/10.1177/1932202x14538975.
Sarnecka, B.W., 2014. On the relation between grammatical number and cardinal numbers in development. Frontiers in Psychology, 5: 1-4. Available at: https://doi.org/10.3389/fpsyg.2014.01132.
Sarnecka, B.W. and S. Carey, 2008. How counting represents number: What children must learn and when they learn it. Cognition, 108(3): 662-674. Available at: https://doi.org/10.1016/j.cognition.2008.05.007.
Sarnecka, B.W., V.G. Kamenskaya, Y. Yamana, T. Ogura and Y.B. Yudovina, 2007. From grammatical number to exact numbers: Early meanings of ‘one’,‘two’, and ‘three’in English, Russian, and Japanese. Cognitive Psychology, 55(2): 136-168. Available at: https://doi.org/10.1016/j.cogpsych.2006.09.001.
Sarnecka, B.W. and M.D. Lee, 2009. Levels of number knowledge during early childhood. Journal of Experimental Child Psychology, 103(3): 325-337. Available at: https://doi.org/10.1016/j.jecp.2009.02.007.
Saxe, G.B., 1977. A developmental analysis of notational counting. Child Development, 48(4): 1512-1520. Available at: https://doi.org/10.1111/j.1467-8624.1977.tb03961.x.
Siegler, R. and M. Robinson, 1982. The development of numerical understandings. In H. Reese, & L. Lipsitt, Advences in child development and behavior. New York: Academic Press, 16: 242-312.
Sophian, C., 1988. Limitations on preschool children's knowledge about counting: Using counting to compare two sets. Developmental Psychology, 24(5): 634-640. Available at: https://doi.org/10.1037/0012-1649.24.5.634.
Starkey, P., E.S. Spelke and R. Gelman, 1983. Detection of intermodel numerical corrospondences by human infants. Science, 222(4620): 179-181. Available at: https://doi.org/10.1126/science.6623069.
Street, B., D. Baker and A. Tomlin, 2005. Navigating numeracies: Home/school numeracy practices. London: Kluwer.
Vygotsky, L., 1998. Thought and languages. (2 Edn.,). (S. Koray, Trans.). Istanbul: Social Transformation Publications.
Wagner, K., K. Kimura, P. Cheung and D. Barner, 2015. Why is number word learning hard? Evidence from bilingual learners. Cognitive Psychology, 83: 1-21. Available at: https://doi.org/10.1016/j.cogpsych.2015.08.006.
Wynn, K., 1990. Children's understanding of counting. Washington D.C: National Science Foundation.
Wynn, K., 1992. Children's acquisition of the number words and the counting system. Cognitive Psychology, 24(2): 220-251. Available at: https://doi.org/10.1016/0010-0285(92)90008-p.
Xu, F. and E.S. Spelke, 2000. Large number discrimination in 6-month-old infants. Cognition, 74(1): B1-B11. Available at: https://doi.org/10.1016/s0010-0277(99)00066-9.
Asian Online Journal Publishing Group is not responsible or answerable for any loss, damage or liability, etc. caused in relation to/arising out of the use of the content. Any queries should be directed to the corresponding author of the article. |