Concept of A.I. Based Knowledge Generator
1Ariel Scientific Innovations (ASI) Ltd, Ariel, Israel
2,3Ariel University, Ariel, Israel
Abstract
An important feature of the currently used artificial intelligence systems is their anthropomorphism. The tool of inductive empirical systems is a neural network that simulates the human brain and operates in the "black box" mode. Deductive analytical systems for representation of knowledge use transparent formalized models and algorithms, for example, algorithms of logical inference. They solve many intellectual problems, the solution of which can do without a "deep" anthropomorphic AI. On the other hand, the solution of these problems leads to the formation of alternative artificial intelligence systems. We propose the formation of artificial intelligence systems based on the following principles: exclusion of black box technologies; domination of data conversion systems: the use of direct mathematical modeling. The base of the system is a simulator - a module that simulates a given object. The ontological module selectively extracts structured sets of functional links from the simulator and fills them with corresponding data sets. The final (custom) representation of knowledge is carried out with the help of special interfaces. The concept of simulation-ontological artificial intelligence, based on the principles outlined above, is implemented in the form of parametric analysis in the configuration space and forms the methodological basis of the AI-platform for e-learning.
Keywords: Artificial intelligence, Knowledge generator, Electronic education, Analytical systems, Simulation modeling, Random generator, Anthology.
JEL Classification: I29
1. Introduction
The base of existing artificial intelligence systems is access to large databases (i.e. with large content), both at the stage of machine learning, and when using these systems. The content of such databases is essentially heterogeneous, and its formation, storage and processing require considerable resources. Systems each time request access data, extract, analyze data and form the content of knowledge.
Each retrieved content unit is actually a product of a special (particular) algorithm, in the form of, for example, proof of a theorem, a computation technique, a software algorithm, etc. If we combine similar (homogeneous) content by certain attributes and create a single algorithm for it in the form of a general simulation model, then this model, with its parametric analysis, makes it possible not only to reproduce the original content, but also to generate new special algorithms, that is, to create a new knowledge. Such knowledge generators, built on the base of simulation-ontological models in the segments of knowledge branches, represent an alternative and at the same time an integrated addition to existing artificial intelligence systems with neural networks and machine learning.
Simulation knowledge generators form stable models of knowledge segments, including databases. When requested, the generator refers to these models, which synthesize the output data (knowledge). Periodically, testing and correction (updating) of models is performed. It is similar to machine learning of neural networks.
2. Methods of Generating Learning Tasks
There are quite a limited number of publications and software products that reflect the use of content generators in the field of electronic education (Posov, 2010). An example is the Math Goodies educational platform, https://www.mathgoodies.com/worksheets, which provides math generated services for junior high school students. This and other similar platforms provide electronic textbooks and problem books on mathematics, physics, including elements of synthesis of multi-variant problems. However, they do not provide an opportunity to generate new knowledge and personalize teaching materials.
Multivariate tasks have different spheres of application. On subsequent attempts of a test task,the student must receive a new assignment, similar to but with differences from those he previously attempted. That is, multivariate tasks will make testing repeatable, thus they solve several problems associated with the testing.
Another application, no less important than the previous ones, is training in solving and fixing skills by solving a large number of tasks on a particular topic. The goal of fixing skills puts strict demands on the differences between tasks of the same type. While for testing (protection) a small change in the assignment that does not affect the content of the task is sufficient, for learning purposes the tasks should be as diverse as possible within the topic that they cover. In other words, when carrying out testing, the complexity of all variants of one job should be the same. When teaching a skill, each new assignment can affect new situations for the student that he has not yet met.
Manual preparation of multivariate tasks is difficult in the first place because of the amount of necessary monotonous work and the errors and misprints that arise. Many instructors independently from each other came up with ways to automate this process and wrote programs to generate options for the tasks they needed. Most generators created by instructors are used only by them, nevertheless from time to time they can share generators or multivariate tasks created with their help with their colleagues.
The first difference between the existing tools is the format for issuing the assignment to the student. Basically, there are two formats: on the computer screen and on paper. Tasks on the computer screen have the advantage that usually the input of the answer is also made on the computer, this allows you to check the answer automatically, to conduct testing remotely, or to take advantage of other features of e-learning systems (Chorng-Shyong et al., 2004). Paper options can be used by most instructors who are not ready to radically change an already established learning process, in which computers are not used.
The second difference is the objects covered by the generators. The most popular is the generation of mathematical tasks, but there are also generators for humanities, more often than not such assignments offer the student closed questions with the choice of answers, comparison of lists, etc.
Instructors who use generators in their practice sometimes talk about this at pedagogical conferences and articles in journals. They describe their generation experience and the technologies used. Sometimes instructors share their generators with each other. Some instructors do not talk about their generation systems on the Internet, but their developments are used by a large number of colleagues at their department or even throughout the university.
To create a generator, you need to prepare a task template - the text of the condition and the response inside which the variables occur, and the program that creates a file with the generated values of the variables on startup. The program can be implemented in any programming language, now they are mostly implemented in Pascal, C ++, some generators are written in Java. The results of generation are compiled and displayed on paper using the computer-aided layout system LaTeX (Leslie, 1994) this allows you to create tasks with complex mathematical formulas.
Creating generators is a complex work and in general, requires programming and implementing algorithms. Nevertheless, some of the examples above show that you can connect instructors and methodologists to the process of creating generators without requiring programming skills from them. For example, it turned out to be done in the GenExis project (Nikitin and Mazurs, 2011). The idea is based on the division of labor between programmers and instructors, the former prepare an editor of generators, and the latter use it to prepare descriptions of generators. Such an approach is called an object-oriented programming, and the language used for describing generators is the language of the domain.
An important task in the study of generation is the development of methods that are both simple enough to use and allow the generation of a wide class of multivariate tasks.
2.1. Simulation-Ontological Models
The subject of the investigation are the methodological and technological foundations for the creation and functioning of expert, reference, training and other artificial intelligence systems based on simulation knowledge generators (Rotkin, 2017). The general simulation-ontological model contains three main options - subject, ontological and interface.
The object model establishes relations between parameters and variables (taken together they are called parameters). It is a multiparametric mathematical model describing the behavior of the objects of the branch of knowledge being studied under the influence of factors. An example model includes a system of I differential equations (f) with J + 1 variables (x, t) and K parameters (p)
![]()
(i=1÷I; j=1÷J; k=1÷K), satisfying the conditions of single-valuedness.
The initial data is formed by special algorithms from the set of corresponding values of the initial parameters. The output data is generated by algorithms from the set of values determined by the model of the values of the output parameters.
The ontological model establishes the relations between the composition and the values of the parameters of the object model, taking into account the constraints imposed on them, and the corresponding data characterizing the objects under study. Algorithms are usually compiled on the basis of numerical (numerical-analytical) methods for analyzing systems of differential equations. Parametric (ontological) analysis of such a system in the general case is a problem of the qualitative theory of differential equations. Interface models convert input and output data of object models to data that provides adequate mapping on graphic, matrix, text and other interfaces. The amount and variety of generated content significantly exceeds the existing knowledge bases, and no significant memory resources are needed, since an extremely large number of combinations of parameters of the simulation model allows to generate unique information without accessing databases. A methodological homogeneity of the received content is important, in contrast to substantially heterogeneous data in knowledge bases. Costs are significantly reduced when creating and operating knowledge generators. In contrast to the existing expert-analytical systems, where highly qualified expert personnel are required at all stages of knowledge generation, in knowledge generators such personnel is needed only at the stage of development of simulation-ontological models. In the operation of generators, the technical staff is mainly used.
Today, while individual specialists are engaged in the stated problem, there are no any noticeable scientific schools, there is no united methodology for generating knowledge. The authors developed a particular (special) concept of simulation generation of analytical content, compiled and tested the appropriate algorithms, based on simulation-ontological models of research and educational projects. Prototypes of expert-analytical systems and, in the context of a real educational process, a number of generators of educational materials were created and tested. Some specific methods of simulation content generation are implemented on the examples of a number of research and educational projects.
2.2. Expert-Analytical Systems
The considered concept and the methodology based on it are used in the creation of analytical systems that are used in the formation of new theoretical developments, in search simulation experiments, for the qualitative presentation of research results. When using the simulation analytical system to study the optimization problems of wind power (Fig. 1), a number of significant effects were revealed (Sokolovsky and Rotkin, 2016). The main task of optimizing the wind turbine as the main element of the power plant is the maximum extraction of the kinetic energy of the air flow passing through the cross section of the engine. With the purpose of obtaining a practical calculation technique, the theory of an ideal windmill is supplemented by particular models of interaction of engine blades with air flow. The basic models, compiled for collinear and orthogonal wind turbines with adjustable blades of linear-convex section, describe almost the entire spectrum of wind turbines used. In mathematical models, aerodynamic relations are used that determine the forces of drag and lift forces of the wing, the adequacy and reliability of which is confirmed by many years of practice.
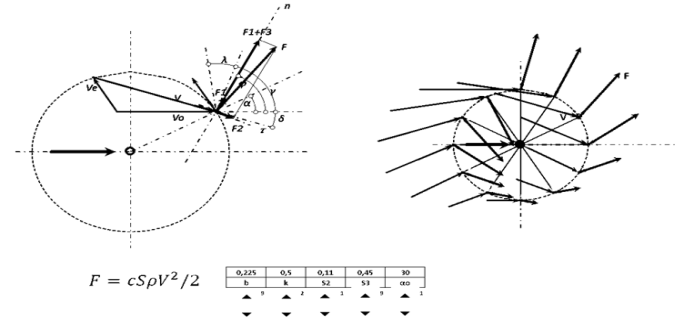
Fig-1. Optimization model of the orthogonal wind turbine.
Analytical simulator
Source: https://youtu.be/AT_z0Y7XfWs
The analytical method developed on the base of the model makes it possible to determine the optimal orientation (configuration) of the turbine blades, calculate the absolute and specific (reduced) energy and power extraction parameters of the air flow. The possibilities, both of an exact analytical approach, and of a multi-factorial numerical experiment are realized.
The indices of the optimal orientation of the blades of the orthogonal turbine essentially depend on the profile of the blades and the speed regime of the turbine. There were revealed significant effects of the inversion of the blade of the orthogonal turbine during its optimization, characterized by abrupt changes in the parameters of orientation (configuration).
As an example of an analytical presentation, a system for localizing sources of artillery (mortar) fire is considered, it reconstructs a ballistic trajectory based on the results of an object scan (Fig. 2). The task of reconstructing the trajectory is relevant when it is necessary to determine the location of the source of the fire and/or the place where the projectile hits. The law of motion of a material point in the field of gravity in the presence of medium resistance is described by differential equations of motion. The parameters of motion can be determined through the coordinates of three points of the trajectory, separated by equal time intervals.
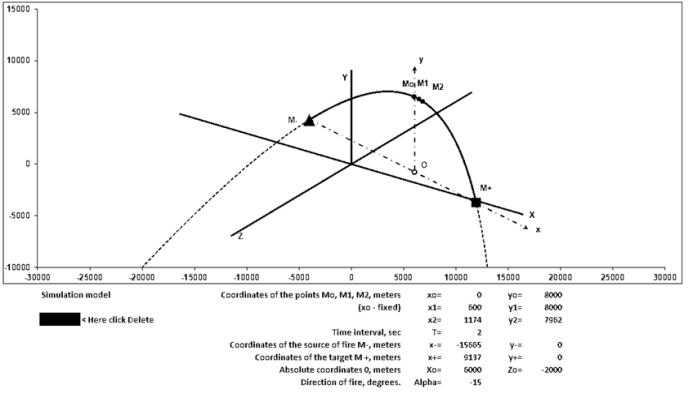
Fig-2. Simulation model of the location of mortar fire.
Elements of the presentation of the content generator.
Source: https://ricent.000webhostapp.com/DomeEn/
Therefore, the above method allows in real time to calculate the motion of an object along a ballistic trajectory, based on the scanning data of the object at three consecutive points. The system can be used both to study the features of the movement of the object, and online, to determine the source of the fire and the point of hit.
2.3. Educational Content Generators
The usage of simulation-ontological modeling in educational projects allows the development of educational platforms of a new generation (Zvolinsky et al., 2017). For example, the section “Point kinematics”; in various courses of disciplines of the “mechanical cycle” assumes the study of the spatial motion of a geometric point given in the time function t by three parametric kinematic equations:
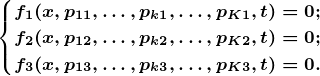
The model defines coordinate functions and their derivatives of different orders, forms linear and nonlinear combinations of functions and their derivatives, determining the various local and integral kinematic characteristics of the object under consideration. Further, the interface model generates the content parameters for its graphical representation to the user (Fig. 3).
The experience of using content generators has defined an adequate form as a duplicate graphic content: on the one hand there is the study material itself (the main) (on the right in Fig. 3), on the other – the same material, reduced for the purpose of monitoring the results of the learning process. Such double forms are used as elements of teaching aids. Being divided into two autonomous parts, one of which is intended for the instructor, this material is used for examinations, interviews and other types of educational control.

Fig-3. Content Generator. The double-form.
Theoretical material "Kinematics of a point", mechanics.
Source:https://ricent.000webhostapp.com/KinPoEn/
The main fundamental feature of the content generator is the parametric nature of the models used in it. This makes it possible, by fixing the values of individual parameters or combinations of them, to isolate from the general simulation model parametric sections particular models of different levels: sections of the course (project), learning disciplines, individual tasks and theorems of different levels of complexity, and finally various numerical and graphics configurations of these problems (Fig.4).
A large number of combinations of parameter values entails an extraordinary variety of generated materials. Ontological options of the simulation model are intended for parametric regulation, with the purpose of extracting content with specified properties. At the same time, it is possible to create a fundamentally new content that is not available in traditional knowledge bases, such as the thematic material “The movement of a natural trihedron”, shown in Fig.3.
After ontological structuring and allocation of particular models, it is advisable to vary free parameters with the help of random number generators in order to obtain configuration variants of tasks, which allows obtaining a unique variant of the task (theorem) for each user.
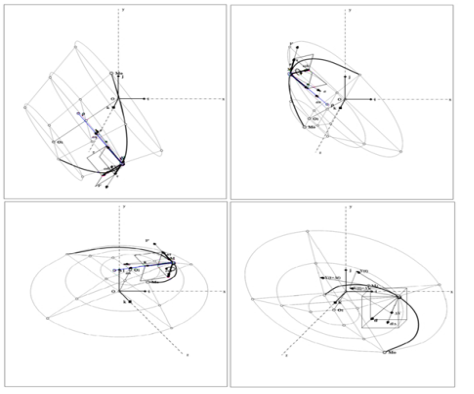
Fig-4. Configurations of theoretical materials “Kinematics of a point”, mechanics.
Source: https://ricent.000webhostapp.com/KinPoEn/
Based on this methodology developed and tested training simulators. For example, the https://ricent.000webhostapp.com/StPrEn+/ link provides a sample of the spatial static object, and https://ricent.000webhostapp.com/StPrEn-/ is a product for controlling acquired skills.
The possibilities of ontological structuring of educational content on various grounds, including the level of complexity, are presented on the example of the problem generator on the topic “Properties of a triangle” in the school course of mathematics (Fig. 5). The basic model (a) contains dozens of parameters characterizing the properties of the object. An extremely large number of parameter combinations allows us to form an almost unlimited number of instructional content problems. For example, in Fig. 5b, the triangle is specified by the side, the median and the angle between them, in Fig. 5c - the median, the bisector and the angle between them, in Fig. 5d - the side, the bisector and the radius of the circumscribed circle. You can vary the tasks by the level of complexity and other characteristics. The use of random number generators allows you to personalize the task on the basis of the level of complexity (at different levels) and offer the user a unique configuration of the task of the selected difficulty level.
Experience in the practical usage of content generators demonstrates the significant impact of simulated content on the didactic features and outcomes of the learning process (Yavich and Davidovich, 2013). First, the study of a certain theoretical material in several significantly different configurations, unlike the typical book, significantly improves the quality of perception of content. This is reflected, for example, in the effective “recognition” of the studied material, both in related branches of knowledge, and in non-obvious practical applications.

Fig-5. Ontological structuring of content.
The topic "Properties of a triangle". School mathematics
Source: https://ricent.000webhostapp.com/TriSimEn/
A significant variety of educational tasks and theorems, with methodological unity and even with external similarity, stimulates users to interact and collaborate, increasing their activity and the amount of perceived information. On the other hand, in the process of joint training activities, leaders are identified, and structuring of users on the level of training and intellectual capabilities that allows them to offer them training materials of different subjects and level of complexity. Such materials as, for example, tasks of increased complexity for independent work, or unique theoretical material for training seminars, are provided on a competitive basis, which stimulates competition among users. In implementing this methodology, the concept of managing the learning process on the basis of network information technologies was used. In particular, the use of mobile communication devices can significantly improve the effectiveness of training sessions. The use of knowledge generators in a limited sphere of the university educational process has shown the possibility and necessity of their improvement for the creation of industry and interbranch systems of knowledge generation based on artificial intelligence.
3. Discussion and Conclusion
The proposed methodology opens up a promising direction in creating a new generation of robotic expert, reference, training and other information and analytical systems. These applications can be used, in particular, to expand the capabilities of various kinds of simulators.
The usage of simulation content generation makes it possible to improve immersion simulation programs by expanding the composition of possible virtual configurations. The total market of immersive simulators is estimated at $ 11 billion. The growth of this market is largely due to the increase in the number of applications in the medical industry, the reduction of risks in the oil and gas industry, and others, through training by the special simulators and many others. Potential users of content generation technology are: Immersive Learning - rapid transfer of knowledge through training in simulators; GSTAT-e-learning marketing and management services; the Ichilov clinic (rehabilitation center) - rehabilitation programs that restore the mobility of people; Media Mobility - analysis, development and implementation of solutions for business customers, and many other organizations.
Given the current state and trends in the development of information technology in the foreseeable future, it is possible reasonably to forecast the substantial development of the proposed technology. Simulation content generators will develop autonomously before filling out their market niche. Subsequently, it seems that complex (cooperative) systems will emerge on the basis of simulation models and the machine learning systems currently used.
References
Chorng-Shyong, O., J.-Y. Lai and Y.-S. Wang, 2004. Factors affecting engineers’ acceptance of asynchronous e-learning systems in high-tech companies. Information & Management, 41(6): 795-804. Available at: https://doi.org/10.1016/j.im.2003.08.012.
Leslie, L., 1994. Latex: A document preparation system. 2 Edn., UK: Pearson Education. pp: 288.
Nikitin, V. and V. Mazurs, 2011. GENEXIS platform and products. 9th International Conference on Emerging eLearning Technologies and Applications (ICETA), Stara Lesna. pp: 153-156.
Posov, I.A., 2010. Programirovanie generatorov zadach (in Russian). Computer tools in Education, 3: 19-31.
Rotkin, V., 2017. Methodology of immanent learning content. Journal Scientific Israel-Technological Advantages, 19(4): 112-118.
Sokolovsky, Y. and V. Rotkin, 2016. Energy efficiency of bladed wind turbine. Optimization model. Journal Scientific Israel - Technological Advantages, 18(2): 111-123.
Yavich, R.P. and N. Davidovich, 2013. Managing student education at the university based on information technology (in Russia). Innovative Proiects and Programs in Education, 2: 69-74.
Zvolinsky, V.P., V.M. Rotkin, V.G. Golovin and N.I. Matveeva, 2017. Automated systems for the formation of educational content (John Russian) / Scientific personal monograph. Volgograd: VSAU. pp: 120.